|
|
|
Estudio analítico y representación gráfica de funciones (EA y RG)
Lo que llamamos estudio analítico de una función, consiste en encontrar su dominio,
hallar sus raíces, determinar dónde crece y dónde decrece, determinar sus
máximos y mínimos relativos, conocer su concavidad, establecer sus puntos singulares.
Todas estas propiedades nos permiten hacer una representación gráfica de la función
muy aproximada a la real. Si tan sólo calculáramos algunos puntos de la gráfica,
tendríamos alguna idea de su variación, pero sería arriesgado unirlos con un
trazo continuo, ya que podrían pasar inadvertidos puntos singulares, por ejemplo.
Para realizar tal análisis de la función, es aconsejable seguir una serie de pasos
ordenados:
- Determinar el dominio.
- Estudiar su continuidad. Hallar asíntotas verticales.
- Hallar sus ceros y determinar su signo.
- Estudiar sus asíntotas horizontales y oblicuas.
- Calcular la derivada primera para hallar extremos (máximos y mínimos), puntos
de inflexión con tangente horizontal y puntos singulares.
- Calcular la derivada segunda para estudiar la concavidad y encontrar los puntos de
inflexión con tangente oblicua.
Se explicará este procedimiento tomando como ejemplo la función
f(x) = xe(x+1)/(x-1)
Dominio
El dominio de una función es el conjunto de valores donde la función
está definida. Se deben hallar los valores de x donde la función no existe. Estos
puntos son:
- Valores donde algún denominador es 0. Se deben hallar las raíces de cada
denominador que aparezca en la función. Esos puntos no pertenecen al dominio.
- Valores donde una cantidad subradical de índice par (por ejemplo raíz cuadrada o
raíz cuarta) es negativa. Se hallan las raíces de la cantidad subradical y se estudia
su signo. Los intervalos donde es negativa son intervalos donde la función no existe.
Las raíces cúbicas (y en general todas las de
índice impar) existen para todos los reales.
- Valores donde algún logaritmando es menor o igual que cero. Se hallan ceros y signo del
logaritmando. Donde sea negativo o cero, la función no existe.
En f(x) = xe(x+1)/(x-1) tenemos un denominador: x - 1. Éste vale 0
cuando x=1. Por lo tanto, f no existe en x=1.
Dominio de f(x) = Df(x) = {x/x pertenece a R ^ x ≠ 1}
Continuidad y asíntotas verticales
De la parte 1) sabemos en qué puntos no existe la función. Ahora tenemos que
averiguar cómo se comporta la función en un entorno de esos puntos. Hallamos los
límites laterales en los puntos de discontinuidad, y en los extremos de los intervalos
de discontinuidad. Si alguno de los límites laterales en un punto x=a da infinito se
dice que f tiene asíntota vertical (AV) de ecuación x=a (ver la página
con las definiciones de asíntotas).
En el ejemplo:
+inf
----^----
lim f(x) = lim xe(x+1)/(x-1) = +inf => f tiene AV x=1.
x->1+ x->1+
-inf
----^----
lim f(x) = lim xe(x+1)/(x-1) = 0+
x->1- x->1-
Podemos comenzar a trazar la función:
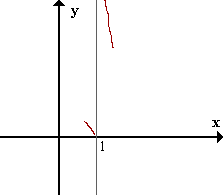
Ceros y signo
Hallar los ceros de la función consiste en resolver la ecuación f(x)=0.
En algunos casos esto no es sencillo, por lo cual puede utilizarse el método de Rolle o
el método de ábacos.
Para especificar el signo se colocan sobre un eje los ceros de la función y los puntos de
inexistencia, y se determina el signo (positivo o negativo) en cada uno de los intervalos que quedan.
En el ejemplo:
f(x) = xe(x+1)/(x-1)
- 0 + E +
-------|-------|------->
0 1
La función exponencial es siempre positiva, para todo exponente real, así que el signo
de f es el signo de x: negativo para x < 0 y positivo para x > 0.
-
En este punto, determinaremos qué asíntotas presenta la función cuando
x tiende a +infinito y -infinito (ver la página sobre asíntotas
para revisar lo básico sobre el tema).
Para ello se debe hallar el límite de la función cuando x tiende a +infinito y -infinito.
- Si limx->inf f(x) = b la función tiene asíntota horizontal de
ecuación y=b (la función se acerca a la recta horizontal y=b cuando x tiende a +infinito
o -infinito).
- Si lim x->inf f(x) = inf
En el ejemplo:
lim f(x) = lim xe(x+1)/(x-1) = +inf
x->+inf x->inf
f(x) xe(x+1)/(x-1)
lim ---- = lim ------------ = e
x->+inf x x->+inf x
lim f(x) - ex = lim xe(x+1)/(x-1) - ex =
x->+inf x->+inf IND. 0.inf
|
lim xe(e(x+1)/(x-1) - 1 - 1) = lim xe(e2/(x-1) - 1) =
x->+inf x->+inf
1 por límites tipo
------^------
(e2/(x-1) - 1) 2 2ex
lim xe.-------------.----- = lim ------ = 2e
x->+inf 2/(x-1) (x-1) x->+inf x - 1
Asíntota: y = ex + 2e
lim f(x) = -inf
x->-inf
f(x)
lim ---- = e
x->-inf x
lim f(x) - ex = 2e
x->-inf
Para x->-inf la asíntota es y = ex + 2e.
Sigamos trazando la gráfica:
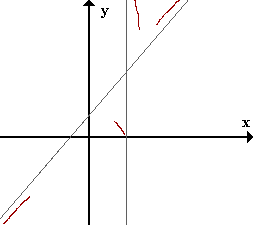
Derivada primera
Se debe calcular la derivada primera, y luego hallar sus ceros y estudiar su signo.
Por información sobre derivación, ver derivada y
reglas de derivación.
Extremos
+ + +
sg f'(x) ----------->
f es creciente
|
|
- - -
sg f'(x) ----------->
f es decreciente
|
|
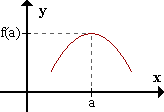
+ 0 -
sg f'(x) -----|----->
a
f presenta un máximo en (a,f(a)).
|
|
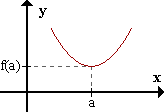
- 0 +
sg f'(x) -----|----->
a
f presenta un mínimo en (a,f(a)).
|
|
Por detalles ver la página sobre variación.
Puntos de inflexión con tangente horizontal
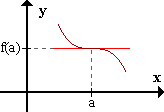
- 0 -
sg f'(x) -----|----->
a
f presenta un punto de inflexión en (a,f(a)) con tangente horizontal.
|
|
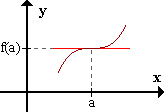
+ 0 +
sg f'(x) -----|----->
a
f presenta un punto de inflexión en (a,f(a)) con tangente horizontal.
|
|
Puntos singulares
E
sg f'(x) -----|----->
a
Si la derivada primera no existe en un punto en que la función sí existe, se dice
que la función presenta un punto singular.
Para averiguar qué tipo de punto singular es, se deben calcular los límites laterales
de la derivada primera en ese punto.
-
lim f'(x) ≠ lim f'(x)
x->a+ x->a-
(los dos finitos y diferentes o a lo sumo uno de ellos infinito.)
La función presenta un punto anguloso en x=a.
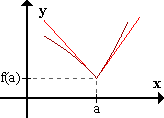
Las tangentes laterales en el punto son diferentes.
Sus ecuaciones son:
y = f'(a)(x-a) + f(a)
----
lim f'(x) y lim f'(x)
x->a+ x->a-
- limx->a+ f'(x) y limx->a- f'(x) son infinitos de distinto signo
(la tangente en dicho punto es vertical).
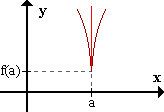
La función presenta un punto de retroceso en x=a.
Estos puntos también son un máximo o un mínimo.
- limx->a+ f'(x) y limx->a- f'(x) son infinitos de igual signo.
La función presenta tangente vertical y es creciente o decreciente.
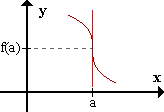
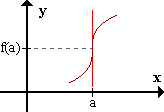
El punto se llama punto de inflexión con tangente vertical.
Continuemos con el ejemplo.
f(x) = xe(x+1)/(x-1)
( x-1-(x+1) )
f'(x) = e(x+1)/(x-1) + xe(x+1)/(x-1)------------- =
(x-1)2
-2x e(x+1)/(x-1)(x2 - 4x + 1)
e(x+1)/(x-1)(----- + 1) = ------------------------
(x-1)2 (x-1)2
__
______ 4+2\|3 __ ~
4 +- \|16 - 4 / ------- = 2 + \|3 = 3,73
------------- = / 2
2 \ __ ~
\ 2-\|3 = 0,27
crec max dec dec min crec
+ 0 - E - 0 +
sg f' -------|-------|-------|------->
__ __
2-\|3 1 2+\|3
__
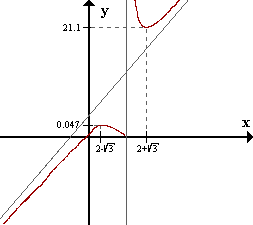
Máximo en (2 - \|3, 0,047)
__
Mínimo en (2 + \|3, 21,1)
Dibujemos ahora esos extremos:
Derivada segunda
Se halla la derivada segunda y luego se hallan sus ceros y signo.
Concavidad
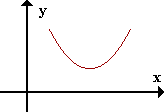
+ +
sg f'' -------->
Si el signo de la derivada segunda es positivo, la función presenta concavidad positiva.
|
|
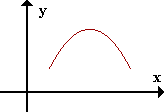
- -
sg f'' -------->
Si el signo de la derivada segunda es negativo, la función presenta concavidad negativa.
|
|
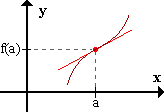
Puntos de inflexión con tangente oblicua
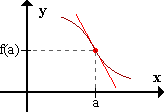
- 0 +
sg f'' ----|---->
a
|
|
|
|
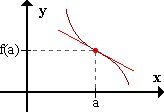
+ 0 -
sg f'' ----|---->
a
|
|
|
|
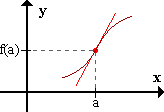
Ecuación de la tangente: y = f'(a)(x-a) + f(a)
Por más información, ver la página sobre concavidad.
En el ejemplo:
(8x - 4)
f''(x) = e(x+1)/(x-1)-------
(x - 1)4
- 0 + E +
sg f'' -----|-----|----->
1/2 1
~
f(1/2) = 0,025
~
f'(1/2) = -2,15
y = -2,15(x-1/2) + 0.025 = -2,15x + 1,1
Finalmente, dibujemos el punto de inflexión:
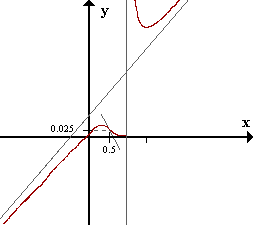
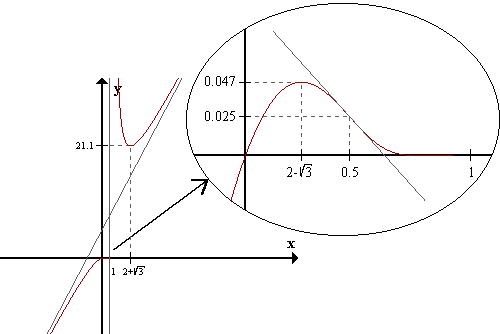
Veamos ahora la gráfica exacta de la función:
|
|
Página principal
Tabla de Contenidos
Noticias matemáticas
|

