Dominio
Lx está definido para x>0 y L|x-1| no está definido en x=1.
Dominio de f: {x/x pertenece a R ^ x>0 ^ x≠1}
Continuidad y asíntotas verticales
lim Lx + L|x-1| + (x2+1)/2 - 2x + 1 = -inf => AV: x=1
x->1+
lim Lx + L|x-1| + (x2+1)/2 - 2x + 1 = -inf => AV: x=0
x->0+
Ceros y signo
Pasaremos por alto este paso pues la ecuación f(x)=0 es difícil de resolver.
Utilizaremos el método de Rolle para aproximar las raíces,
luego de que contemos con la información de los ceros y el signo de la derivada primera.
Asíntotas horizontales y oblicuas
lim Lx + L|x-1| + (x2+1)/2 - 2x +1 = +inf
x->+inf (por órdenes de infinitos)
0 0 +inf
-^- --^-- --^-- +inf
Lx L|x-1| (x2+1) -^-
lim --- + ------ + -------- - 2x + 1 = lim x/2 - 2x =
x->+inf x x 2x x->+inf
lim -3x/2 = -inf
x->+inf
DA paralela al eje oy.
|
|
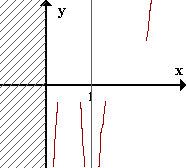
Dominio de f: x>0 y x≠1.
AV: x=1 y x=0.
DA || oy para x->+inf.
|
Derivada primera
1 1 2x x3 - 3x2 + 4x - 1 g(x)
f'(x) = --- + ---- + -- - 2 = ----------------- = ------
x x-1 2 x(x-1) x(x-1)
Para determinar ceros y signo de g(x), utilizaremos el método de Rolle:
g'(x) = 3x2 - 6x + 4
_______
6 + \|36 - 48
------------- no pertenece a R
6
+ + +
sg g' -----------> => g es creciente
lim g(x) = +inf
x->+inf
- 0 +
sg g --------|-------->
α
Aproximaremos la raíz α de g(x) con dos dígitos decimales:
g(0) = -1 |
> g(0.5) = 0.375
g(1) = 1 | g(0.4) = 0.184 ~
g(0.3) = -0.043 => α = 0.35
- 0 +
sg g --------|-------->
0.35
+ 0 - 0 +
sg x(x-1) -----|-----|----->
0 1
Combinando el signo de g(x) y el signo de x(x-1), tenemos el
signo de f'(x):
E + 0 - E +
sg f' -/-/-/-/-|-----|-----|----->
0 0.35 1
~
f(0.35) = -0.62
Máximo en (0.35,-0.62).
Ceros y signo
Con la información obtenida en el cálculo de asíntotas, podemos determinar
el signo de f a la derecha de 0, en un entorno de 1 y cuando x->+inf.
También sabemos que en 0.35 la función tiene un máximo, y su valor es -0.62.
E - - - E - +
sg f -/-/-/-/-|-----|-----|----->
0 0.35 1
Vemos que f sólo puede tener raíces mayores que 1. Observando el signo de f',
vemos que f es creciente a la derecha de 1, por lo tanto sólo puede tener una raíz.
Aproximando se llega a que la raíz es 1.85.
E - E - 0 +
sg f -/-/-/-/-|-----|-----|----->
0 1 1.85
Derivada segunda
(3x2-6x+4)(x)(x-1) - (x3-3x2+4x-1)(2x-1)
f''(x) = --------------------------------------- =
x2(x-1)2
x4-2x3-x2+2x-1 h(x)
-------------- = ------
x2(x-1)2 x2(x-1)2
Para determinar ceros y signo de h(x), utilizaremos el método de Rolle:
h'(x) = 4x3 - 6x2 - 2x + 2
h''(x) = 12x2 - 12x - 2
~
________ = 1.14
12 + \|144 + 96 /
--------------- \ ~
24 = -0.14
+ 0 - 0 +
sg h'' ----------|----------|---------->
-0.14 1.14
h'(-0.14) > 0 y h'(1.14) < 0
lim h'(x) = +inf y lim h'(x) = -inf
x->+inf x->-inf
- 0 + 0 - 0 +
sg h' -----|-----|-----|-----|-----|----->
α -0.14 β 1.14 γ
Por aproximación, hallamos α, β y γ:
~
α = -0.65
~
β = 0.45
~
γ = 1.65
h(-0.65) < 0, h(0.45) < 0 y h(1.65) < 0
lim x4 = +inf
x->+inf
+ 0 - - - - - - - 0 +
sg h -----|-----|-----|-----|-----|----->
α -0.65 0.45 1.65 β
~
α = -1.15
~
β = 2.15
El denominador de f'', x2(x-1)2, es siempre positivo,
salvo en 0 y 1 donde vale 0, y por lo tanto f'' no existe.
E - E - 0 +
sg f'' -/-/-/-/-|-----|-----|----->
0 1 2.15
~
f(2.15) = 0.41
Punto de inflexión en (2.15, 0.41)
~
f'(2.15) = 1.48
y = 1.48(x-2.15) + 0.41
Tangente en el punto: y = 1.48x - 2.77
|
|
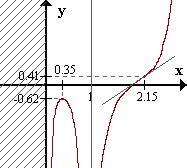
Raíz: 1.85.
Máximo en (0.35, -0.62).
Punto de inflexión en (2.15, 0.41).
- Tangente en el punto: y = 1.48x - 2.77.
|
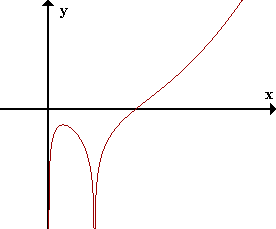
Por último, corroboremos nuestro análisis observando la gráfica exacta de la función: