• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Teorema de Bolzano

Antes de enunciar el teorema de Bolzano, veamos una definición y una propiedad relativas a sucesiones, que se emplearán en la demostración de dicho teorema. (Por más detalles, visitar la página sobre sucesiones).

Definición: Par de sucesiones monótonas convergentes (PSMC)

((a_n),(b_n)) es un PSMC <=>
1) (a_n) es creciente
    (b_n) es decreciente
2) Para todo n natural a_n < b_n
3) Para todo ε > 0 existe h natural / b_h - a_h < ε

Propiedad: Todo PSMC tiene frontera

((a_n),(b_n)) es un PSMC => existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

Teorema de Bolzano

Bernhard Bolzano (1781-1848)

Si una función f(x) es continua en un intervalo cerrado [a,b] y f(a) y f(b) son de distinto signo, existe por lo menos un punto entre a y b para el cual f(c)=0.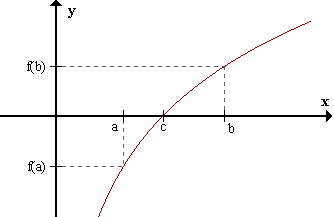

H) f(x) continua en [a,b]
    f(a).f(b) < 0
T) Existe c perteneciente a (a,b) / f(c) = 0

Geométricamente, el teorema establece que si dos puntos (a,f(a)) y (b,f(b)) de la gráfica de una función continua están situados en diferentes lados del eje x, entonces la gráfica intersecta al eje en algún punto entre a y b. Por supuesto que pueden haber varias intersecciones.

Demostración:

Supongamos que f(a)<0 y f(b)>0. (La demostración sería análoga si supusiéramos f(a)>0 y f(b)<0.)

Consideremos el punto medio de [a,b]: (a+b)/2.
Si f((a+b)/2)=0 queda demostrado el teorema. Sino, f será positiva o negativa en (a+b)/2.

Tomemos una de las mitades del intervalo [a,b] donde la función sea negativa en un extremo y positiva en el otro. Llamemos a₁ y b₁ a los extremos de este intervalo. Ahora dividamos [a₁,b₁] a la mitad. Si f no vale cero en el punto medio, será positiva o negativa. Tomemos la mitad donde f tiene distinto signo en cada extremo, y llamemos a estos puntos a₂ y b₂.

Si continuamos de esta manera, obtenemos una sucesión de intervalos [a,b], [a₁,b₁], [a₂,b₂], etc., tales que a <= a₁ <= a₂ <= ... <= a_n y b >= b₁ >= b₂ >= ... >= b_n.

Es decir,
1) Los a_i forman una sucesión creciente y los b_i forman una sucesión decreciente.
2) Los a_i son siempre menores que los b_i.

Veamos cuál es el lim_n->+inf b_n - a_n.

bn - an es la longitud del intervalo [a_n,b_n].
La longitud del intervalo [a₁,b₁] es (b - a)/2, la mitad de la longitud de [a,b] que es b - a.
La longitud del intervalo [a₂,b₂] es (b - a)/2², la mitad de la longitud de [a₁,b₁] que es (b - a)/2.
Y siguiendo de esta manera, la longitud del intervalo [a_n,b_n] es (b - a)/2ⁿ.

De modo que,
3) lim_n->+inf b_n - a_n = lim_n->+inf (b - a)/2ⁿ = 0.

1), 2) y 3) son las condiciones de la definición de PSMC:

• a_n es creciente, b_n es decreciente
• Para todo n natural a_n < b_n
• Para todo ε>0 existe h natural / b_h - a_h < ε (que es lo mismo que lim_n->+inf b_n - a_n = 0.)

Todo PSMC tiene la propiedad de definir un número frontera entre ambas sucesiones.

((a_n),(b_n)) es un PSMC => existe c / para todo n a_n <= c <= b_n, lim a_n = c- y lim b_n = c+.

lim a_n = c- significa que para todo δ>0 existe n₁ / para todo n>=n₁ c - δ < a_n < c.
lim b_n = c+ significa que para todo δ>0 existe n₂ / para todo n>=n₂ c < b_n < c + δ.

O sea que tomando el mayor entre n₁ y n₂, llamémosle n₃, se cumplen ambas cosas.
Es decir, para todo δ>0 existe n₃ / para todo n >= n₃ c-δ < [a_n,b_n] < c+δ.

Esto significa que, para cualquier entorno de c que consideremos, existe un intervalo [a_n,b_n] contenido en dicho entorno.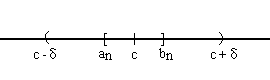

Por otro lado, f es continua en [a,b] por hipótesis. Por lo tanto es continua en c. Por definición de continuidad, lim_x->c f(x)=f(c).

Si f(c)<0, por teo. de conservación del signo existe un entorno de c donde f(x) es negativa.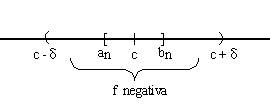

Dentro de este entorno, existe un intervalo [a_n,b_n], donde f(a_n) es de distinto signo que f(b_n). Esto es una contradicción, por lo tanto f(c) no puede ser negativo.

Si f(c)>0, por teo. de conservación del signo existe un entorno de c donde f(x) es positiva.

Pero, otra vez, dentro de ese entorno existe un intervalo [a_n,b_n] tal que f(a_n) es de distinto signo que f(b_n).

Por lo tanto, no existe otra posibilidad: f(c)=0.

Propiedad de Darboux

Gaston Darboux (1842-1917)

Si una función f(x) es continua en un intervalo cerrado [a,b] y k es cualquier número entre f(a) y f(b), entonces existe un valor d entre a y b para el cual f(d)=k.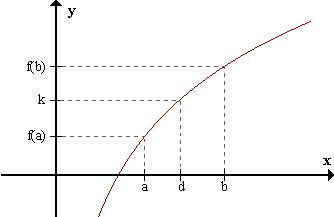

H) f continua en [a,b]
   f(a) < k < f(b)
T) Existe d perteneciente a (a,b) / f(d)=k

Sea g una función auxiliar: g(x) = f(x) - k.

1. g es continua en [a,b] por ser suma de funciones continuas
2. g(a) = f(a) - k < 0
3. g(b) = f(b) - k > 0

=> de 1), 2) y 3) por teorema de Bolzano, existe d perteneciente a (a,b) / g(d) = f(d) - k = 0

O sea, existe d perteneciente a (a,b) / f(d)=k.

<< anterior    siguiente >>

Cálculo > Continuidad

Definición – Bolzano y Darboux – Weierstrass