• CÁLCULO
• Límites
• Continuidad
• Asíntotas
• Derivada
• Variación
• EA y RG
• Sucesiones y series
• MATEMÁTICA DISCRETA
• Enteros
• Conteo
• Principio del Palomar
• OTROS TEMAS
• Lugares geométricos

Teoremas de Rolle y de Lagrange

Teorema de Rolle

Michael Rolle (1652-1719)

Si una función es continua en un intervalo cerrado [a,b], derivable en el intervalo abierto (a,b) y f(a)=f(b), entonces existe al menos un punto c entre a y b para el cual f'(c)=0.

H) f es continua en [a,b]
    f es derivable en (a,b)
    f(a)=f(b)
T) Existe c perteneciente a (a,b) / f'(c)=0

Interpretado geométricamente, significa que si una curva alcanza el mismo valor en dos puntos, entonces debe poseer una tangente horizontal en algún punto intermedio.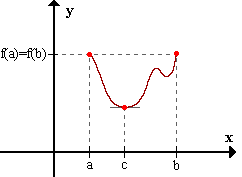

Demostración:

f es continua en [a,b] => por teo. de Weierstrass f tiene máximo absoluto M y mínimo absoluto m en [a,b].

Para todo x perteneciente a [a,b] m <= f(x) <= M.

Existe x₁ perteneciente a [a,b] / f(x₁)=M.

Existe x₂ perteneciente a [a,b] / f(x₂)=m.

Si m = M => para todo x perteneciente a [a,b] f(x) = M => f'(x) = 0

Sino, m < M => por lo menos uno de los puntos, x₁ o x₂, corresponde al interior del intervalo, a (a,b), por ejemplo x₂.

=> (a,b) se comporta como un entorno de x2.

Se cumple que para todo x perteneciente a (a,b) f(x₂) <= f(x)

=> Por def. de mínimo relativo f presenta un mínimo relativo en x₂. (1)

f es derivable por hipótesis. (2)

De 1) y 2), por Condición necesaria para la existencia de extremos relativos f'(x₂)=0

Teorema de Lagrange o del valor medio

Joseph Louis Lagrange (1736 - 1813)

Si f(x) es continua en el intervalo cerrado [a,b] y derivable en todo punto del intervalo abierto (a,b), entonces existe al menos un punto c donde f'(c) = (f(b) - f(a))/(b - a).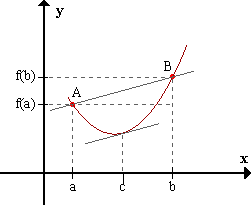

H) f(x) es continua en [a,b]
    f(x) es derivable en (a,b)
T) Existe c perteneciente a (a,b) / f'(c)=(f(b) - f(a))/(b - a)

Geométricamente, (f(b) - f(a))/(b - a) es la tangente del ángulo que forma la secante que pasa por los puntos A(a,f(a)) y B(b,f(b)) de la curva, con el eje ox.
f'(c) es la tangente del ángulo que forma la recta tangente a la curva en el punto c, con el eje ox.

Entonces, el teorema expresa que existe al menos un punto en el intervalo (a,b) donde la tangente a la curva es paralela a la recta que pasa por A y B.

Demostración:

Definamos una función auxiliar g(x) = f(x) + hx, h perteneciente a R.

g es continua en [a,b] por ser suma de funciones continuas.
g es derivable en (a,b) por ser suma de funciones derivables.
Queremos que g(a) sea igual a g(b) para aplicar el teorema de Rolle
=> f(a) + ha = f(b) + hb => f(a) - f(b) = hb - ha = h(b - a)

       f(a) - f(b)   
=> h = -----------
          b - a

=> por teo. de Rolle, existe c perteneciente a (a,b) / g'(c) = 0

g'(x) = f'(x) + h
                                  f(b) - f(a)
g'(c) = f'(c) + h = 0 => f'(c) =  -----------
                                     b - a

Considérese por ejemplo, el caso donde x es el tiempo y f(x) la distancia de un automóvil desde su punto de partida a lo largo de cierto camino.
Entonces (f(b) - f(a))/(b - a) es la velocidad promedio del automóvil en el período b - a. (Recordar que velocidad = distancia/tiempo)
Por lo tanto f'(a)=lim_x->a (f(x) - f(a))/(x - a) es la velocidad del auto en el tiempo a.
Si por ejemplo el auto ha recorrido 200km. en 2 hs., la velocidad promedio fue de 100km. por hora.
Por el teorema de Lagrange podemos decir que, al menos en un momento durante esas dos horas, el auto tuvo una velocidad de exactamente 100km/h.

<< anterior  siguiente >>

Cáculo > Derivada

Definición – Reglas de derivación – Rolle y Lagrange – Cauchy y L'Hôpital